Question

the radius of one circular field is 5m and that of other is 3m.find the radius of circular field whose area is the difference of the areas of the first and second field.​

Answer 1

4m

Explanation:

1. Recall the formula for area of a circle for each calculation
2. Calculate the area of the large field (r = 5m)
3. Calculate the area of the small field (r = 3m)
4. Find the difference in area
5. Find the radius of the "difference" field using difference in area

The formula for area of a circle is A = πr².

"A" means area.

π is pi. I will use the π button, but some teachers ask to use 3.14.

"r" means radius.

Area of large field:

Substitute "r" for 5m in the formula.

A = πr²

A = π(5m)²

A = π25m²

A = 78.5398163397 m²

Area of small field:

Substitute "r" for 3m in the formula.

A = πr²

A = π(3m)²

A = π9m²

A = 28.2743338823 m²

Difference in areas:

Subtract the area of small field from the area of large field.

(78.5398163397 m²) - (28.2743338823 m²)

= 50.2654825 m²

Radius of "difference" field:

Since we are looking for radius, not area, rearrange the formula to isolate "r".

A = πr²

`(A)/(\pi )` =
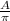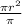`(\pi r^(2))/(\pi)` Divide both sides by π

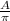`(A)/(\pi )` = r² π cancels out on the right side

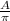`(A)/(\pi )` = √r² Square root both sides

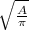`\sqrt{(A)/(\pi )}` = r ² and √ cancel out, leaving "r" isolated

r =
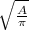`\sqrt{(A)/(\pi )}` Variable on the left for standard formatting

Substitute "A" for the difference in area

r =
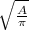
`\sqrt{(A)/(\pi )}`

r =
`\sqrt{(50.2654825m^(2))/(\pi )}` Divide by pi first

r =
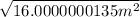`\sqrt{16.0000000135 m^(2)}` Find the square root

r ≈
`4m`

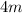
The radius of the field that has the area of the difference in the two fields is 4m.