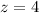Question

If x

`\infty`
yz, and when y=-2, z=-3, x=30. when y=4, x=80. find z
​

Answer 1

Answer:
`z = 4`

Explanation:

Given:

`x \alpha yz`

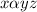
replacing the proportionality sign with a constant , we have :

`x = kyz`

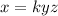
substituting :
`y = -2` ,
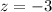`z = -3` and
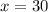`x = 30` into the equation , we have :

`30 = k(-2)(-3)`

`30 = 6k`

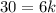
divide through by 6

`k = 5`

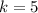
substituting
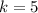`k = 5` into the equation , the equation becomes

`x = 5yz`

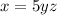
To find the value of z , when y = 4 , x = 80 , we will substitute the values into the formula , we have :

`80 = 5(4)(z)`

`80 = 20z`

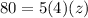
dividing through by 20 , we have :

`z = 4`