Question

One of the roots of the quadratic equation x2−5mx+6m2=0 is 36. Find the greatest possible value of the second root. Help needed as soon as possible, Thank You.

Answer 1

The greatest possible value of the second root, β = 54

Explanation:

The given quadratic equation is:

`x^2-5mx+6m^2=0`

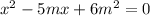
Let α and β be the roots of the given quadratic equation.

α = 36

To find, the greatest possible value of the second root ( β) = ?

∴ The sum of the roots,

α + β =
`(-b)/(a)`

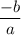
⇒ 36 + β =
`(-(-5m))/(1)`

⇒ 5m = 36 + β ............. (1)

The product of the roots,

α.β =
`(c)/(a)`

⇒
`36.\beta=(6m^2)/(1)`

⇒
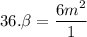
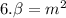`6.\beta=m^2` ............. (2)

From equations (1) and (2), we get

⇒
`((36+\beta)/(5))^(2)=6\beta`

⇒
`\beta^2-78\beta+1296=0`

⇒
`\beta^2-54B\beta-24B\beta+1296=0`

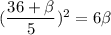
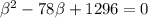
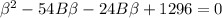
⇒ β(β - 54) - 24(β - 54) = 0

⇒ (β - 54)(β - 24) = 0

⇒ β - 54 = 0 or, β - 24 = 0

⇒ β = 54 or, β = 24

∴ The greatest possible value of the second root, β = 54