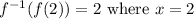a) f (2) = 1
b)
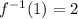
c)
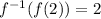
Explanation:
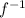 - Indicates that we have to find the inverse of the function
- Indicates that we have to find the inverse of the function
Given data:
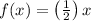 --------> eq.1
--------> eq.1
 ---------> eq.2
---------> eq.2
To find
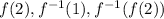
Case a)
Now, substitute x = 2 in the equation 1 to find f (2)
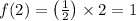
Case b)
Now, substitute x = 1 in the equation 2 to find
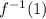
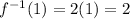
Case c)
In general,
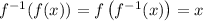
Thereby,