Question

H(x)=1/2x^3−x^2

What is the average rate of change of h over the interval −2≤x≤2?

Answer 1

The average rate of change is 2

Solution:

Given that we have to find the rate of change

The average rate of change is given as:

`Rate\ of\ change = (f(b)-f(a))/(b-a)`

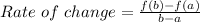
Given function is:

`h(x) = (1)/(2)x^3 -x^2`

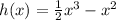
Given interval is:

`-2\leq x\leq 2`

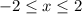
Therefore,

a = -2 and b = 2

Thus formula becomes:

`Rate\ of\ change = (h(2)-h(-2))/(2-(-2))\\\\Rate\ of\ change = (h(2)-h(-2))/(4) ----- eqn 1`

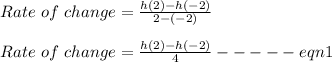
Find h(2)

Substitute x = 2 in given function

`h(2) = (1)/(2) * 2^3 - 2^2\\\\h(2) = 2^2-2^2 = 0`

Find h(-2)

Substitute x = -2 in given function

`h(-2) = (1)/(2) * (-2)^3 -(-2)^2\\\\h(-2) = -4 -4 = -8`

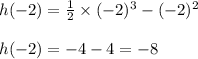
Substitute the values in eqn 1

`Rate\ of\ change = (0-(-8))/(4)\\\\Rate\ of\ change =(8)/(4) = 2`

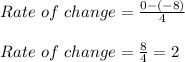
Thus average rate of change is 2