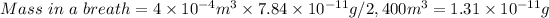Question

In an unhealthy, dusty cement mill, there were 2.6 by 10^9 dust particles (sp gr=3) per cubic meter of air. Assuming the particles to be spheres of 2 micrometers diameter, calculate the mass of dust a) in a 20m by 15m by 8m room and b) inhaled in each average breath of 400cm3 volume

Answer 1

a) 7.9×10⁻¹¹ g (rounded to 2 significant figures)

b) 1.3×10⁻¹⁷ g (rounded to 2 significant figures)

Step-by-step explanation:

A) Mass of dust in the room

• Volume of the room

`Volume=length* width* height=20m* 15m* 8m=2,400m^3`

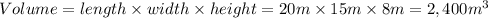
• Number of particles of dust in the room

`Number\text{ }of\text{ }particles=density\text{ }of\text{ }particles* Volume`

`Number\text{ }of\text{ }particles=2.6* 10^9particles/m^3* 2,400m^3= 6.24* 10^(12)particles`

• Volume of a particle

`Volume\text{ }of\text{ }a\text{ }spehere=4/3\pi r^3=4/3\pi (2*10^(-6)/2m)^3=4.1889* 10^(-18)m^3`

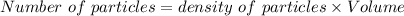
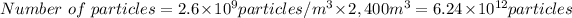
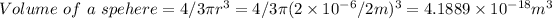
• Volume of 2.6×10⁹ particles

`Volume=6.24* 10^(12)particles* 4.1889*10{-18}m^3/particle=2.61* 10^(-5)m^3`

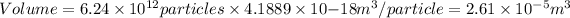
• Mass of 2.6×10⁹ particles

Density = 1.00 g/cm³ × sp gr = 1.00 g/cm³ × 3 = 3.00 g/cm³

Density = 3.00 g/cm³ × (1m/100cm)³ = 3.00×10⁻⁶ g/m³

`Mass=density* volume=3.00* 10^(-6)g/m^3* 2.61*10^(-5)m^3=7.84*10^(-11)g`

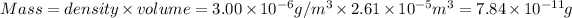
B) Mass of dust in each average breath of 400cm³

• Convert 400cm³ to m³: 4.00×10⁻⁴ m³

• Set a propotion

`Mass\text{ }in\text{ }a\text{ }room/2,400m^3=Mass\text{ }in\text{ }a\text{ }breath/4* 10^(-4)m^3`

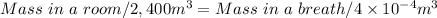
• Solve for Mass in a breath

`Mass\text{ }in\text{ }a\text{ }breath=4*10^(-4)m^3* 7.84* 10^(-11)g/2,400m^3=1.31* 10^(-11)g`