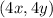Question

Which rule yields the dilation of the figure RSTU centered at the origin?

A) (x, y) → (4x, 4y)
B) (x, y) → (0.25x, 0.25y)
C) (x, y) → (x + 4, y + 4)
D) (x, y) → (x + 0.25, y + 0.25)

Answer 1

A is correct

Explanation:

Answer 2

Answer: OPTION A.

Explanation:

Dilation is defined as transformations in which the Image (The figure obtained after the transformation) and the Pre-Image (The original figure) have the same shape, but their sizes are different.

For a dilation using a scale factor "k" and centered at the origin, the rule is:

`(x.y)` →
`(kx,ky)`

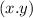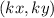
Let's pick the point S of the Pre-Image RSTU. This is :

`S(1,1)`

And the point S' of the Image R'S'T'U' is:

`S'(4,4)`

You can identify that the coordinates of S' are obtained by multiplying the coordinates of the point S by this scale factor:

`k=4`

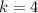
Therefore, the rule that yields this dilation is:

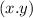`(x.y)` →
`(4x, 4y)`