Option A:
ΔDEF
 ΔABC; x = 1.5; CB = 3.9; AB = 3;
ΔABC; x = 1.5; CB = 3.9; AB = 3;

Solution:
Each pair of given polygons are similar.
Similarity statement for the given polygons:
In ΔDEF and ΔABC,
∠D = ∠A (Angle)
∠E = ∠B (Angle)
Therefore, ΔDEF
 ΔABC (by AA similarity)
ΔABC (by AA similarity)
If two triangles are similar, then their sides are proportional.
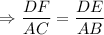
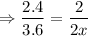
Do cross multiplication,
⇒ 2.4 × 2x = 2 × 3.6
⇒ 4.8x = 7.2
⇒ x = 1.5
Substitute x = 1.5 in CB and AB,
CB = 3x – 0.6
= 3(1.5) – 0.6
CB = 3.9
AB = 2x
= 2(1.5)
AB = 3
Scale factor means ratio of the sides of the triangle.
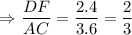
Therefore, Option A is the correct answer.
Hence ΔDEF
 ΔABC; x = 1.5; CB = 3.9; AB = 3;
ΔABC; x = 1.5; CB = 3.9; AB = 3;
 .
.