Question

I need help with these 2 questions

Question: By completing the square, solve for x in the following equations:

a)

`x {}^(2) - 6x + 4 + = 0`
b)

`4x {}^(2) + 16x + 9 = 0`
​

Answer 1

see explanation

Explanation:

(a)

x² - 6x + 4 = 0 ( subtract 4 from both sides )

x² - 6x = - 4

To complete the square

add ( half the coefficient of the x- term )² to both sides

x² + 2(- 3)x + 9 = - 4 + 9

(x - 3)² = 5 ( take the square root of both sides )

x - 3 = ±
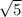`√(5)` ( add 3 to both sides )

x = 3 ±
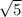`√(5)` ← exact solutions

(b)

4x² + 16x + 9 = 0

To complete the square

The coefficient of the x² term must be 1

Factor out 4 from 4x² + 16x

4(x² + 4x) + 9 = 0

add/subtract ( half the coefficient of the x- term )² to x² + 4x

4(x² + 2(2)x + 4 - 4 ) + 9 = 0

4(x + 2)² - 16 + 9 = 0

4(x + 2)² - 7 = 0 ( add 7 to both sides )

4(x + 2)² = 7 ( divide both sides by 4 )

(x + 2)² =
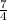`(7)/(4)` ( take the square root of both sides )

x + 2 = ±
`\sqrt{(7)/(4) }` = ±
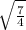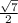`(√(7) )/(2)` ( subtract 2 from both sides )

x = - 2 ±
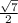`(√(7) )/(2)` ← exact solutions