Question

Find an equation of the set of all points equidistant from the points A(−1, 5, 3) and B(4, 1, −3). Describe the set. a cube with diagonal AB a plane perpendicular to AB a line perpendicular to AB a sphere with diameter AB

Answer 1

Answer:Plane perpendicular to line AB

Step-by-step explanation: let consider a point C (x,y,z) which is equidistant from the point A and B.

So the distance D can be written as

D=AC=
`\sqrt((x+1)^2+(y-5)^2+(z-3)^2)`

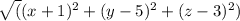
D=BC=
`\sqrt((x-4)^2+(y-1)^2+(z+3)^2`

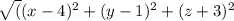
The two Ds can be equated into one equation

`\sqrt((x+1)^2+(y-5)^2+(z-3)^2)` =
`\sqrt((x+1)^2+(y-5)^2+(z-3)^2)`

`(x+1)^2+(y-5)^2+(z-3)^2=(x-4)^2+(y-1)^2+(z+3)^2`

`x^2+2x+1+y^2-10y+25+z^2-6z+9=x^2-8x+16+y^2-2y+1+z^2+6z+9`

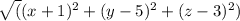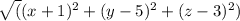
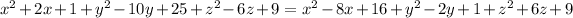
Cancelling the x,y,z squares and simplifying

`2x-10y-6z+35=-8x-2y+6z+26`

`10x-8y+12z+9=0`

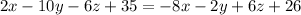
This equation is of the line perpendicular to AB.

which can be seen by for example putting z=0 in the equation

`8y=10x+9`

the slope of the line is then

`m=10/8`

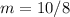
m=5/4

while the slope between the x any y in the points AB is

`m=(5-1)/(-1-4)`

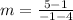
m=-4/5

so the plane is perpendicular.

I would add a little further explanation

that is if you imagine this in 2d the points equal distance from any line AB are points on the line in the middle of AB that is perpendicular to AB.

In the 3d that line becomes the plane in between the line AB which is perpendicular