Question

PLEASE PLEASE ANSWER!

Find the area of the shaded regions below. Give your answer as a completely simplified exact value in terms of π (no approximations).

Answer 1

The area of the shaded region is
`$8(\pi \ -√(3))\ \text{cm}^2`.

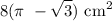Solution:

Given radius = 4 cm

Diameter = 2 × 4 = 8 cm

Let us first find the area of the semi-circle.

Area of the semi-circle =
`(1)/(2)* \pi r^2`

`$=(1)/(2)* \pi* 4^2`

`$=(1)/(2)* \pi* 16`

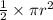
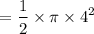
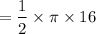
Area of the semi-circle =
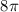`$8\pi` cm²

Angle in a semi-circle is always 90º.

∠C = 90°

So, ABC is a right angled triangle.

Using Pythagoras theorem, we can find base of the triangle.

`AC^2+BC^2=AB^2`

`AC^2+4^2=8^2`

`AC^2=64-16`

`AC^2=48`

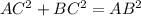
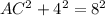
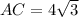`AC=4√(3)` cm

Base of the triangle ABC =
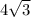`4√(3)` cm

Height of the triangle = 4 cm

Area of the triangle ABC =
`(1)/(2)* b * h`

`$=(1)/(2)* 4√(3) * 4`

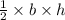
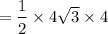
Area of the triangle ABC =
`8√(3)` cm²

Area of the shaded region

= Area of the semi-circle – Area of the triangle ABC

=
`$8\pi \ \text{cm}^2-8√(3)\ \text{cm}^2`

=
`$8(\pi \ -√(3))\ \text{cm}^2`

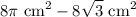
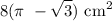
Hence the area of the shaded region is
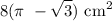`$8(\pi \ -√(3))\ \text{cm}^2`.