Answer:
Approximately
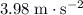 .
.
Assumption: air resistance on the rocket is negligible. Take
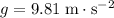 .
.
Step-by-step explanation:
By Newton's Second Law of Motion, the acceleration of the rocket is proportional to the net force on it.
 .
.
Note that in this case, the uppercase letter
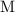 in the units stands for "mega-", which is the same as
in the units stands for "mega-", which is the same as
 times the unit that follows. For example,
times the unit that follows. For example,
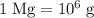 , while
, while
 .
.
Convert the mass of the rocket and the thrust of its engines to SI standard units:
- The standard unit for mass is kilograms:
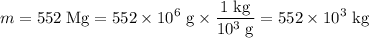 .
. - The standard for forces (including thrust) is Newtons:
 .
.
At launch, the velocity of the rocket would be pretty low. Hence, compared to thrust and weight, the air resistance on the rocket would be pretty negligible. The two main forces that contribute to the net force of the rocket would be:
- Thrust (which is supposed to go upwards), and
- Weight (downwards due to gravity.)
The thrust on the rocket is already known to be
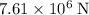 . Since the rocket is quite close to the ground, the gravitational acceleration on it should be approximately
. Since the rocket is quite close to the ground, the gravitational acceleration on it should be approximately
 . Hence, the weight on the rocket would be approximately
. Hence, the weight on the rocket would be approximately
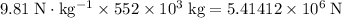 .
.
The magnitude of the net force on the rocket would be
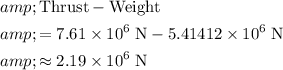 .
.
Apply the formula
 to find the net force on the rocket. To make sure that the output (acceleration) is in SI units (meters-per-second,) make sure that the inputs (net force and mass) are also in SI units (Newtons for net force and kilograms for mass.)
to find the net force on the rocket. To make sure that the output (acceleration) is in SI units (meters-per-second,) make sure that the inputs (net force and mass) are also in SI units (Newtons for net force and kilograms for mass.)
 .
.