Question

Consider the following equation of the form dy/dt = f(y)dy/dt = ey − 1, −[infinity] < y0 < [infinity](a) Sketch the graph of f(y) versus y.(b) Determine the critical (equilibrium) points, and classify each one as asymptotically stable or unstable. (Enter your answers as a comma-separated list. If there are no critical points in a certain category, say NONE.)(c) Draw the phase line.(d) Sketch several graphs of solutions in the ty-plane.

Answer 1

Complete Question:

The complete question is shown on the first uploaded image

Answer:

a) The graph of f(y) versus y. is shown on the second uploaded image

b) The critical point is at y = 0 and the solution is asymptotically unstable.

c)The phase line is shown on the third uploaded image

d) The sketch for the several graphs of solution in the ty-plane is shown on the fourth uploaded image

Explanation:

Step One: Sketch The Graph of f(y) versus y

Looking at the given differential equation

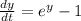`(dy)/(dt) = e^(y) - 1` for -∞ <
`y_(o)` < ∞

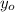We can say let
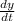`(dy)/(dt)` = f(y) =
`e^(y) - 1`

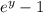
Now the dependent value is f(y) and the independent value is y so to sketch is graph we can assume a scale in this case i cm on the graph is equal to 2 unit for both f(y) and y and the match the coordinates and after that join the point to form the graph as shown on the uploaded image.

Step Two : Determine the critical point

To fin the critical point we have to set
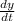`(dy)/(dt)` = 0

This means
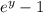`e^(y) - 1` = 0

For this to be possible
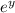`e^(y)` = 1

which means that
`e^(y)` =
`e^(0)`

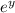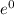
which implies that y = 0

Hence the critical point occurs at y = 0

meaning that the equilibrium solution is y = 0

As t → ∞, our curve is going to move away from y = 0 hence it is asymptotically unstable.

Step Three : Draw the Phase lines

A phase line can be defined as an image that shows or represents the way an ODE(ordinary differential equation ) that does not explicitly depend on the independent variable behaves in a single variable. To draw this phase line , draw the y-axis as a vertical line and mark on it the equilibrium, i.e. where f(y) = 0.

In each of the intervals bounded by the equilibrium draw an upward

pointing arrow if f(y) > 0 and a downward pointing arrow if f(y) < 0.

This phase line would solely depend on y does not matter what t is

On the positive x axis it would get steeper very quickly as you move up (looking at the part A graph).

For below the x-axis which stable (looking at the part a graph) we are still going to have negative slope but they are going to be close to 0 and they would take a little bit longer to get steeper

Step Four : Draw a Solution Curve

A solution curve is a curve that shows the solution of a DE (deferential equation)

Here the solution curve would be drawn on the ty-plane

So the t-axis(x-axis) is its the equilibrium that is it is the solution

If we are above the x-axis it is going to increase faster and if we are below it is going to decrease but it would be slower (looking at part A graph)