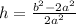Question

This description assumes the elliptic object is centered at (0, 0). However, since the elliptic object is not fixed, initially in the animation it is placed at (0, H) and starts to fall down due to gravity. It then hits the supporter and eventually reaches a stable equilibrium. When the elliptic object settles stably on the supporter, its center position is at (0, h). Derive a formula to compute h using the elliptic parameters a and b.

Answer 1

Complete Question

The complete question is shown on the first and second uploaded image

Answer:

The derived
`h = (b^(2) - 2a^(2) )/(2a^(2))`

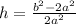
Explanation:

Step One : Consider the ellipse in equilibrium.

Looking at the ellipse in equilibrium i.e when the ellipse has settled down on the concave support (represented by a parabola ) as shown on the third uploaded image.

Step Two : Consider the ellipse equation.

Generally the equation of the ellipse is given as

`(x^(2))/(a^(2)) + ((y-h)^(2))/(b^(2))\\`

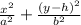
Also the base on which it rest at equilibrium i.e the parabola is represented by
`y = x^(2) -1`

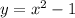
Substituting the value of y in the ellipse equation we have

`(x^(2))/(a^(2))+ ((x^(2)-1-h)^(2))/(b^(2))=1`

Let
`x^(2) = t`

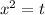
So the equation becomes

`(t)/(a^(2)) + ((t -1 -h)^(2))/(b^(2)) =1`

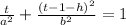
Rearranging, we get :

`a^(2) t^(2) + (b^(2)- 2a^(2)(h +1))t + a^(2)((h +1 )^(2) -b^(2) =0`

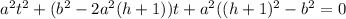
This equation above is a quadratic equation or a bi-quadratic equation in x as t =
`x^(2)`

Step Three : Relate the equation an the graph on the third uploaded image

We can see that from the graph , if A and B are the two values of x for which the points is made , then A + B = 0 (because they are symmetric in nature)

From Vieta's Roots(Vieta's formula is a formula that shows the relationship between the coefficients of a polynomial and the sum of its roots )

`ax^(2) + bx + c =0`

with A and B as roots

A+B =
`(-b)/(a)`

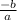
But A + B = 0

So
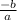`(-b)/(a)` = 0

or we can say that

`(b^(2) - 2a^(2)(h +1 ))/(a^(2))`

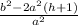
Rearranging we get

`h = (b^(2)- 2a^(2))/(2a^(2))`