Answer:
The new frequency (F₂ ) will be related to the old frequency by a factor of one (1)
Step-by-step explanation:
Fundamental frequency = wave velocity/2L
where;
L is the length of the stretched rubber
Wave velocity =
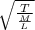
Frequency (F₁) =
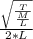
To obtain the new frequency with respect to the old frequency, we consider the conditions stated in the question.
Given:
L₂ =2L₁ = 2L
T₂ = 2T₁ = 2T
(M/L)₂ = 0.5(M/L)₁ = 0.5(M/L)
F₂ =
![\frac{\sqrt{(2T)/(0.5((M)/(L)))}}{4*L} = \frac{\sqrt{4((T)/((M)/(L))})}{4*L} = (2)/(2) [\frac{\sqrt{(T)/((M)/(L))}}{2*L}] = F_1](https://img.qammunity.org/2021/formulas/physics/college/1bg2c80vxcasib2oeghju5ysv05ittme97.png)
Therefore, the new frequency (F₂ ) will be related to the old frequency by a factor of one (1).