Answer:
3 kilometers per hour
Explanation:
Please consider the complete question.
Hong swam 8 kilometers against the current in the same amount of time it took him to swim kilometers 16 with the current. The rate of the current was 1 kilometer per hour. How fast would Hong swim if there were no current?
Let x represent Hang's swimming rate.
Hang's rate upstream would be:

Hang's rate downstream would be:
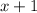
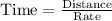
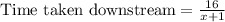
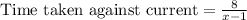
Since downstream and upstream times are equal, so we can equate both equation as:
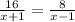
Cross multiply:
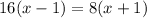
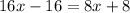
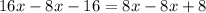
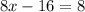
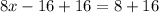
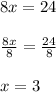
Therefore, Hong would swim at a rate of 3 kilometers per hour, if there were no current.