Question:
Samir’s family has decided to purchase an above-ground cylindrical swimming pool for his backyard. The best space that they have for a pool measures 360 cm across. The tallest pool that they can buy is 120 cm high.
a) What is the volume of the largest pool that they can buy? Give your answer in cubic centimeters.
b) The walls on the pool inflate to be 10 cm thick, but the bottom of the pool is just a thin piece of vinyl. What would the full capacity of this pool be?
c) The manufacturer’s instructions warn that the pool should only be filled to 90% of its capacity. How much water would it take to fill the pool 90%? Give your answer in liters.
Answer:
a)Volume of the cylindrical pool = 12200000
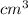
b) Capacity = 10889520 cm³
c) 90% of capacity = 9800568 litres
Explanation:
Given:
Radius of the pool = 360 cm
Height of the pool = 120 cm
A) The volume of the largest pool that they can buy
Volume of cylindrical pool =
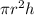
where
r is the radius of the pool
h is the height
But we have diameter = 360 cm
Radius =
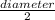
Radius =
Radius = 180 cm
On substituting the values
Volume of the cylindrical pool =
Volume of the cylindrical pool = 12200000
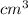
B)The full capacity of this pool be
Capacity of pool = volume of inside pool
Diameter of inside of pool = diameter of outside of pool – thickness of 2 walls
Diameter of inside of pool = 360 cm – (2 x 10) cm
Diameter of inside of pool = 360 -20 cm
Diameter of inside of pool = 340 cm
Now
Radius =
=
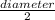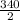= 170 cm
Volume of inside of pool (capacity) =
Capacity = 10889520 cm³
C)water it would take to fill the pool 90
90% of capacity = Volume of the pool x 90%
90% of capacity =
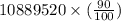
90% of capacity = 10889520 \times 0.9
90% of capacity = 9800568
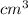or 9800.568 litres