Question

The pressure, temperature, and density of a flow are SLS conditions. Assuming isentropic flow, if the temperature at another point in the flow increases to 600°R, calculate the pressure and density at this new point. 2. Calculate the total/stagnation conditions (density, pressure, temperature) of the flow in #1 above. 3. Calculate the airspeed of the flow at points 1 and 2 in #1. 4. The freestream conditions in an isentropic flow moving at 300 m/s are SLS conditions. If the local pressure at a point along the airfoil drops to 0.5 atm, calculate the local airspeed at that point. 5. If we used Bernoulli’s Equation to solve for #3, what would the local velocity be? What is the percent difference from your results in #3?

Answer 1

1. ρ₂ = 1.76 kg/m³ , P₂ = 168.699 kPa

2. T₀ = 345.75 K, P₀ = 191.742 kPa, ρ₀= 1.93 kg/m³

3. V₁ = 340.26 m/s , V₂ = 365.96 m/s

4. the local airspeed at 0.5 atm point = 308.2 m/s

5. The percentage difference is = 6.98 % ≈ 7 %

Step-by-step explanation:

Pressure, P = 101.325 kPa

Density = 1.225 kg/m³

Temperature, T = 288.15 K = 518.67 °R

Gas constant of air, Rair = 287.057 J/(kg·K)

1. Thus since the density, ρ₁ at sea level standard, SLS = 1.225 kg/m³

T₁ = 288.15, γ = 1.005, T₂ = 600 °R = 333.33 K

ρ₂ = ρ₁×
`((T_(2) )/(T_(1) )) ^{(1)/(\gamma - 1) }`

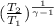
= 1.225×
`((333.33)/(288.15)) ^{(1)/(1.4 - 1) }`

= 1.76 kg/m³

Similarly the pressure P₂ is given by
`P_(1) ((T_(2) )/(T_(1) )) ^{(\gamma)/(\gamma - 1) }`

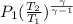
From where P₁ = 101.325 kPa hence P₂ = 168.699 kPa

2). Speed =
`√(kRT)`

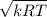
= Where R = 287.057 J/(kg·K)

Hence speed =
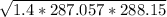`√(1.4*287.057*288.15)` = 340.26 m/s

Therefore T₀ = T₁ +
`(V_(1) ^(2) )/(2C_(p) )`

= 288.15 + 340.26²/(2×1.005))×(1/1000) = 345.75 K

Therefore as we have

`P_(0) = P_(1) ((T_(01) )/(T_(1) )) ^{(1)/(\gamma - 1) }`

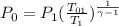
, P₀ =101325 ×(345.75/288.15)^(1.4/(1.4-1)

= 191.742 kPa

and ρ₀ = ρ₁ ×
`((T_(01) )/(T_(1) )) ^{(1)/(\gamma - 1) }`

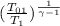
ρ₁ = 1.225 kg/m³, T₀ = 345.75 K, T₁ = 288.15 K

∴ ρ₀= 1.93 kg/m³

3.) The speed is given as Speed =
`√(kRT)`

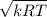
Hence at 1 speed as previously calculated = 340.26 m/s

while at 2 speed =
`√(1.4*287.057*333.33)`

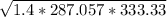
= 365.96 m/s

4.) If the speed drops to 0.5 atm we have

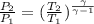`(P_(2) )/(P_(1) ) =((T_(2) )/(T_(1) )) ^{(\gamma)/(\gamma - 1) }` from where P₂/P₁ = 101.325 kPa/ 50.6625 kPa = 0.5 hence

0.5 =
`((T_(2) )/(288.15 )) ^{(1.4)/(1.4 - 1) }`

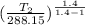
From where T₂ = 236.4 K

Hence speed =
`√(kRT)` =

=
`√(1.4*287.057*308.2)`

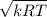= 308.2 m/s

5.) With Bernoulli's equation we have

We have ΔP/ρ -v₁²/2 = -v₂²/2

Hence we have (101.325 kPa -168.699 kPa )/1.225 kg/m3 - (340.26 m/s )²/2 = -v₂²/2

or v₂ = 340.42 m/s

The percentage difference is 100* (365.96 m/s - 340.42 m/s)/365.96 m/s = 6.98 % ≈ 7 %