Question

Determine which score corresponds to the higher relative position. Which is better, a score of 92 on a test with a mean of 71 and a standard deviation of 15, or a score of 688 on a test with a mean of 493 and a standard deviation of 150?

Answer 1

The score of 92 on a test with a mean of 71 and a standard deviation of 15 is better.

Explanation:

To find which score corresponds to the higher relative position, we find the Z-score of each score.

The z-score, which measures how many standard deviation a measure is above or below the mean, is given by the following formula:

`Z = (X - \mu)/(\sigma)`

In which X is the score,
`\mu` is the mean and
`\sigma` is the standard deviation.

A score of 92 on a test with a mean of 71 and a standard deviation of 15.

So
`X = 92, \mu = 71, \sigma = 15`

`Z = (X - \mu)/(\sigma)`

`Z = (92 - 71)/(15)`

`Z = 1.4`

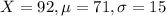
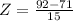
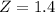
A score of 688 on a test with a mean of 493 and a standard deviation of 150.

So
`X = 688, \mu = 493, \sigma = 150`

`Z = (X - \mu)/(\sigma)`

`Z = (688 - 493)/(150)`

`Z = 1.3`

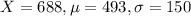
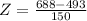
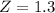
Which is better?

Due to the higher z-score, the score of 92 on a test with a mean of 71 and a standard deviation of 15 is better.