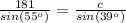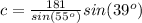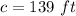Question

another person is on the ground looking up at the tower at an angle of 55 degrees. How far is the person from the tower?

Answer 1

Part A) The height of the tower is 181 feet

Part B) The person is 139 feet from the tower

Explanation:

The complete question is

The leaning tower of Pisa in Italy makes an angle of 86 degrees with the ground. a person standing on the ground approximately 82 feet from the tower at an angle of 69 degrees.

Part A) how tall is the tower?

Part B) Another person is on the ground looking up at the tower at an angle of 55 degrees. How far is the person from the tower?

Part A) see the attached figure to better understand the problem

step 1

Find the measure of angle C

we know that

The sum of the interior angles in any triangle must be equal to 180 degrees

so

in the triangle ABC

`m\angle A+m\angle B+m\angle C=180^o`

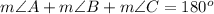
substitute the given values

`86^o+69^o+m\angle C=180^o`

`m\angle C=180^o-155^o=25^o`

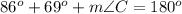
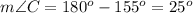
step 2

Find the measure of b

Applying the law of sines

`(b)/(sin(B))=(c)/(sin(C))`

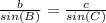
substitute the given values

`(b)/(sin(69^o))=(82)/(sin(25^o))`

`b=(82)/(sin(25^o))sin(69^o)`

`b=181\ ft`

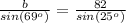
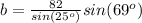
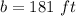
Part B) Another person is on the ground looking up at the tower at an angle of 55 degrees. How far is the person from the tower?

step 1

Find the new measure of angle C

in the triangle ABC

`m\angle A+m\angle B+m\angle C=180^o`

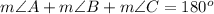
Find the measure of c

substitute the given values

`86^o+55^o+m\angle C=180^o`

`m\angle C=180^o-141^o=39^o`

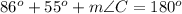
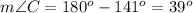
step 2

Find the measure of c

Applying the law of sines

`(b)/(sin(B))=(c)/(sin(C))`

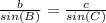
we have

`b=181\ ft\\C=39^o\\B=55`

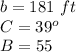
substitute the values

`(181)/(sin(55^o))=(c)/(sin(39^o))`

`c=(181)/(sin(55^o))sin(39^o)`

`c=139\ ft`