Question

If a charge is located at the center of a spherical volume and the electric flux through the surface of the sphere is Φ, what would be the flux through the surface if the radius of the sphere were tripled?

A) theta/9
B) 3theta
C) 9theta
D) theta
E) theta/3

Answer 1

D) theta

Step-by-step explanation:

The electric flux is the electric field multiplied the area that the E-field passes through, Φ = EA.

The area of a sphere is 4πR^2, and the electric field of a point particle is given by the following formula.

`E = (1)/(4\pi\epsilon_0)(Q)/(r^2)`

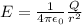
Now we can compare the flux in both cases.

`\Theta_1 = (1)/(4\pi\epsilon_0)(Q)/(R^2)4\pi R^2 = (Q)/(\epsilon_0)\\Theta_2 = (1)/(4\pi\epsilon_0)(Q)/((6R)^2)4\pi(6R)^2 = (Q)/(\epsilon_0)`

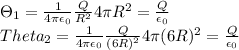
As can be seen from above, the electric flux would not change if the radius of the sphere were tripled.

Another approach to this question is to use Gauss’ Law. According to Gauss’ Law, the electric flux is equal to the enclosed charge divided by electric permittivity. Since the enclosed charge is constant in this question, the electric flux remains constant as well.