Question

If the velocity v of a particle moving along a straight line decreases linearly with its displacement s from 19 m/s to a value approaching zero at s = 39 m, determine the acceleration a of the particle when s = 8 m and show that the particle never reaches the 39-m displacement.

Answer 1

Explanation:The rate of decrease of velocity is given with respect to displacement. As v approaches zero when s approaches 39, it can be written as

`(dv)/(ds) =-19/39\\m=(dv)/(ds)\\Hence\\v=ms+c\\`

where c=19

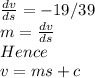
`v=-(19)/(39) *s+19\\`

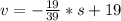
when s=8 we have

`v=-(19)/(39) * 8 +19\\v=15.1 m/s`

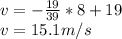
hence a can be found by the chain rule

`a=(ds)/(dt) (dv)/(ds)\\a=v*(dv)/(ds)\\a=15.1 *-(19)/(39)\\a=7.357 m/s^2`

From the equation

`v=-(19)/(39) *s+19\\`

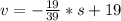
the s in term of t can be found

`v=(ds)/(dt) \\\int\limits {v} \, dt =\int\limits {} \, ds\\\int\limits {-(19)/(39) *s+19} \, dt=\int\limits {} \, ds\\\\\int\limits^t_0 {} \, dt=\int\limits^s_0 {(1)/(-(19)/(39) *s+19) } \, ds`

`t=-(39)/(19) ln((s-39)/(39) )\\`

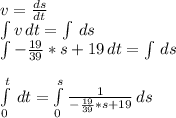
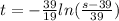
Hence it can be seen that if s approaches 39 the t function becomes undefined hence s is never 39m