Question

Homer wants to identify the center and radius of the circle defined by the equation x2 + y2 - 14x +

2y – 25 = 0. He follows these steps:
Step 1: (x² – 14x) + (y2 + 2y) = 25
Step 2: (x2 – 14x +49) + (y2 + 2y + 1) = 25
Step 3: (x – 7)2 + (y + 1)2 = 25
Step 4: The center is (7,-1), and the radius is 5.
At which step did Homer make a mistake, and what was it?​

Answer 1

step 2

Explanation:

Answer 2

Homer has made mistake in step 2

When you complete the square, you need to add the values to both sides of equation

Solution:

Given equation of circle:

`x^2 + y^2 -14x + 2y -25 = 0`

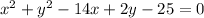
Let us first calculate center and radius and find out where he did the mistake

Step 1:

Group the terms

`x^2 -14x + y^2 + 2y = 25\\\\(x^2 -14x) + (y^2 + 2y) = 25`

Step 2:

`(x^2 -14x + 49) + (y^2 + 2y + 1) = 25 + 49 + 1`

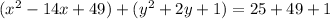
But homers step 2 is:

`(x^2 -14x + 49) + (y^2 + 2y + 1) = 25`

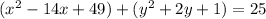
So homer has made mistake in this step

When you complete the square, you need to add the values to both sides of equation

But homer did not add 49 and 1 to right side of equation

Correct steps are:

`(x^2 -14x + 49) + (y^2 + 2y + 1) = 75\\\\(x-7)^2 + (y+1)^2 = 75`

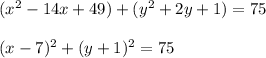
Comparing general equation of circle,

`(x-h)^2 + (y-k)^2 = r^2`

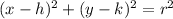
Therefore, center is ( 7, -1) and radius is 8.66