Answer:
The probability that 5 or fewer women are hired, assuming no gender discrimination, is 0.0317; we can use this result to support her charge of gender discrimination.
Explanation:
If we are assuming that the women and the men are equally qualified, then the probability for each employee that is hired the probability for it to be a women should be 1/2. Note that the fact that more men that women are hired in a sample might not be disctrimination: for example, if 2 men are hired out of 2 employees, that can happen with probability 1/4, so it is quite common. In order to support her charge for gender discrimination, we need at least a probability less that 0.05 that 5 (or less) women are hired out of 19 employees.
Since each configuration is equally probable, we will count the total amount of possible cases that 5 or less women are hired, and dividide it by the total amount of cases, 2¹⁹.
- 0 women hired: one possible case: every employee is male
- 1 women hired: 19 possible cases
- 2 women hired:
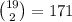possible cases - 3 women hired:
possible cases - 4 women hired:
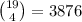possible cases - 5 women hired:
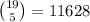possible cases
Thus, there are a total of 11628+3876+969+171 = 16644 possible cases out of 2¹⁹ ones. All of them with seemingly equal probability. As a consequence, the probability of 5 or less women to be hired out of 19 employees, assuming that the probability to hire 1 is 1/2, is
16644/2¹⁹ = 0.0317 < 0.05
The probability that 5 or fewer women are hired, assuming no gender discrimination, is 0.0317. Since the probability is so low, we can conclude that for the employer, a woman equally qualified as a man is less likely to be hired, therefore, we can support her charge of gender discrimination.