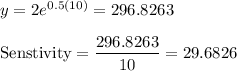Answer:
At x = 0, Sensitivity = Not defined
At x = 1, Sensitivity = 3.2974
At x = 2, Sensitivity = 2.71825
At x = 5, Sensitivity = 4.8729
At x = 10, Sensitivity = 29.6826
Explanation:
We are given the following in the question:
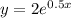
where y is the output and x is the input of a system.
We define sensitivity as the ration of output to input.
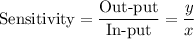
At x = 0

At x = 1
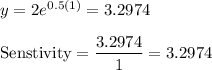
At x = 2
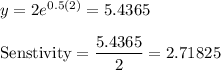
At x = 5
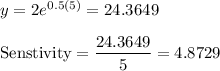
At x = 10