Answer:
Minimum time interval (t2)=0.90 SECONDS
Step-by-step explanation:
- coefficient of friction for employees footwear = 0.5
- coefficient of friction for typical athletic shoe = 0.810
- frictional force = coefficient of friction X acceleration due to gravity X mass of body
- Acceleration due to gravity is a constant = 9.81 m/s
- Let frictional force for employee footwear = FF1
- Let frictional force for athletic footwear =FF2
FF1 = O.5 X 9.81 X mass of body
= 4.905 x mass of body
FF2 = 0.810 X 9.81 X mass of body
= 7.9461 x mass of body
The body started from rest there by making the initial velocity zero ( u = 0)
From d= ut + 1/2 a x

- d =
 x a x
x a x
 .....................................i
.....................................i
where d= distance and it is given as 3.25m
- F =ma ...................................ii
making acceleration subject of the formula from equation ii
- a =
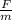
Making t subject of formula from equation (i)
- t=
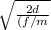
where
-
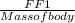 = 4.905
= 4.905
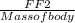 =7.9461
=7.9461
Let
- t1 = minimum time taken for frictional force for employee foot wear
- t1 =
 =1.15 seconds
=1.15 seconds
- t2 =
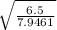 = 0.90 seconds
= 0.90 seconds
THANK YOU