Question

The length of a rectangle is 3 m more than twice the width, and the area of the rectangle is 54 mº. Find the dimensions of the rectangle.

Answer 1

• The dimensions of rectangle are 12 m and 4.5 m

Explanation:

Given :-

• The length of a rectangle is 3 m more than twice the width
• the area of the rectangle is 54 m²

To find :-

• Dimensions of rectangle

Solution:-

According to the question ,

Let the width of rectangle be x and length of rectangle be 2x+3 m

Area of rectangle :- L×B

L×B = 54m²

(2x+3) * x = 54m²

x = 4.5 m

By putting the value of x , we get

Length :- 2x+3 = 12 m

Width :- 4.5 m

Answer 2

• The dimensions of rectangle are 12 m and 4.5 m

Explanation:

Given that, The length of a rectangle is 3 m more than twice the width, and the area of the rectangle is 54 m²

Let's assume width of rectangle be x m and length be 3 + 2x m respectively. To find the dimensions of the rectangle we will use the formula of Perimeter of rectangle

`\\ { \underline{ \boxed{ \pmb{ \sf{ \purple{Area _((rectangle)) = Length × width}}}}}} \\ \\`

Substituting values in above formula:

`\\ \dashrightarrow \sf \: \: (3 + 2x)(x) = 54 \\`

`\dashrightarrow \sf \: \: 3x + 2x^2 = 54 \\`

`\dashrightarrow \sf \: \: - 54 + 3x + 2x^2 = 0 \\`

`\dashrightarrow \sf \: \: 2x^2 + 3x - 54 = 0\\`

`\dashrightarrow \sf \: \: 2x^2 + 12x - 9x - 54 = 0\:`

`\dashrightarrow \sf \: \: 2x(x + 6) -9(x + 6) = 0\\`

`\dashrightarrow \sf \: \: (2x -9)(x+6) = 0 \\`

`\sf{x=}{\sf{(9)/(2)}}{\sf{\: or\: -6}}`

`\dashrightarrow \: \: { \underline{ \boxed{ \pmb{ \sf{\purple{ x = 4.5 }}}}}}`

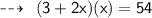
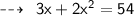
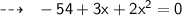
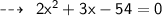
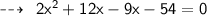
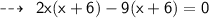
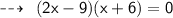
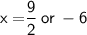
Hence,

• Length of rectangle = 3 + 2x = 3 + 2(4.5) = 12 m
• Width of the rectangle = x = 4.5m

`\\ { \underline{ \pmb{ \frak{ \therefore Length \: and \: width \: of \: the \: rectangle \: is \:12 \: m \: and \: 4.5 \: m}}}} \\`