Question

Given the equation, what is the center and radius of the circle?
(X-2) ^2+ (Y+11)^2=100

Answer 1

Center: (2, -11)

Radius: 10

Explanation:

(x - 2)² + (y + 11)² = 100

(x - h)² + (y - k)² = r²

-------------------------------

x - 2 = 0

+2 +2

x = 2

------------

y + 11 = 0

-11 -11

y = -11

------------------------------

r² = 100

r = √100

r = 10

----------------------------

Center: (h, k)

Radius: r

-------------------------------

Center: (2, -11)

Radius: 10

I hope this helps!

Answer 2

We are given the equation of circle (x - 2)² + (y + 11)² = 100 , but let's recall the standard equation of circle i.e (x - h)² + (y - k)² = r², where (h, k) is the centre of the circle and r being the radius ;

So, consider the equation of circle ;

`{:\implies \quad \sf (x-2)^(2)+(y+11)^(2)=100}`

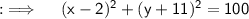
Can be further written as ;

`{:\implies \quad \sf (x-2)^(2)+\{y-(-11)\}^(2)={10}^(2)}`

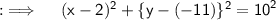
On comparing this equation with the standard equation of Circle, we will get, centre and radius as follows

• Centre = (2, -11)
• Radius = 10 units