Question

A carbon-dioxide laser emits infrared light with a wavelength of 10.6 μm

a. What is the length of a tube that will oscillate in the m = 100,000 mode?
b. What is the frequency?
c. Imagine a pulse of light bouncing back and forth between the ends of the tube. How many round trips will the pulse make in each second?

Answer 1

0.53 m

`2.8301886792* 10^(13)\ Hz`

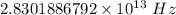
283286118.98

Step-by-step explanation:

c = Speed of light =
`3* 10^8\ m/s`

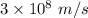
m = Mode = 100000

`\lambda` = Wavelength =
`10.6\ \mu m`

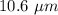
Length of a tube is given by

`L=m(\lambda)/(2)\\\Rightarrow L=100000(10.6* 10^(-6))/(2)\\\Rightarrow L=0.53\ m`

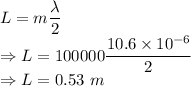
The length of the tube is 0.53 m

Frequency is given by

`f=(c)/(\lambda)\\\Rightarrow f=(3* 10^8)/(10.6* 10^(-6))\\\Rightarrow f=2.8301886792* 10^(13)\ Hz`

The frequency is
`2.8301886792* 10^(13)\ Hz`

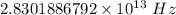
Time taken to bounce back and forth

`t=(2L)/(c)\\\Rightarrow t=(2* 0.53)/(3* 10^8)\\\Rightarrow t=3.53* 10^(-9)\ s`

Round trips in one second

`n=(1)/(3.53* 10^(-9))\\\Rightarrow n=283286118.98`

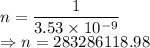
The number of round trips is 283286118.98