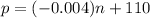Question

A clothing business finds there is a linear relationship between the number of shirts, n , it can sell and the price, p , it can charge per shirt. In particular, historical data shows that 19000 shirts can be sold at a price of $ 34 , while 24000 shirts can be sold at a price of $ 14 . Give a linear equation in the form p = m n + b that gives the price p they can charge for n shirts

Answer 1

Linear equation is p = (-0.004) n + 110

Explanation:

We have, p = price, n = no. of shirts , m = slope,

b = constant (y - intercept)

linear equation as ,
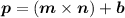`\boldsymbol{p}=(\boldsymbol{m} * \boldsymbol{n})+\boldsymbol{b}` .....(1)

(p,n)= ($34, 19000) & ($14, 24000)

putting above values in equation (1) we get,

⇒ 34 = (19000×m) + b ⇒
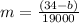`m=((34-b))/(19000)` .... (2)

and, 14 = (24000×m) + b ⇒
`m=((14-b))/(24000)` ....(3)

Equating equations (2) & (3),

⇒
`((14-b))/(24000)=((34-b))/(19000)`

⇒
`((14-b))/(24)=((34-b))/(19)`

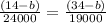
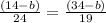
⇒ 19 (14 – b) = 24 (34 – b)

⇒
`(19 * 14)-19 b=(24 * 34)-24 b`

⇒
`24 b-19 b=-(19 * 14)+(24 * 34)`

⇒
`5 b=-(19 * 14)+(24 * 34)`

⇒
`5 \mathrm{b}=-266+816=550`

⇒
`\mathrm{b}=(550)/(5)=110`

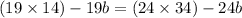
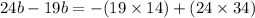
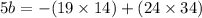
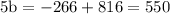
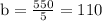
⇒ b = 110

Now,
`m=((14-110))/(24000)=(-96)/(24000)=-0.004`

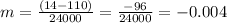
putting values of m & b in equation (1) we get :

`p=(-0.004) n+110`