Question

A small rocket is fired from a launchpad 15 m above the ground with an initial velocity left angle 400,450,600 right angle ​m/s. A crosswind blowing to the north produces an acceleration of the rocket of 3 m divided by s squared. Assume the​ x-axis points​ east, the​ y-axis points​ north, the positive​ z-axis is vertical​ (opposite g), and the ground is horizontal. Answer parts a through d.

a. Find the velocity and position vectors for t greater than or equal to 0.
b. Make a sketch of the trajectory.
c. Determine the time of flight and range of the object.
d. Determine the maximum height of the object.

Answer 1

a)

v=<400, 450+3t, 600-9.81t> m/s

r=<400t, 450t+3
`t^(2)`/2, 15+600t-9.81
`t^(2)`/2> m/s

b) attach file

c) t=122.324s

d) z=18369.9854 m

Explanation:

a)

The equation for velocity of each component is v=
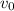`v_(0)`+at, in this case the x-axis component has acceleration 0
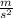`(m)/(s^(2) )`, the y-axis component has acceleration 3
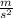`(m)/(s^(2) )` and the z-axis component has -g
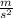`(m)/(s^(2) )`, where g=9.81
`(m)/(s^(2) )`.

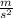The equation for position of each component is x=
`x_(0)`+
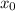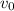`v_(0)`t+a
`t^(2)`/2,

with <
`x_(0)`,
`y_(0)`,
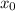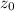`z_(0)`>=<0,0,15>.

c) This time is t when z=0, with positive sign.

d)Solving the equation
`V_f^(2)`=
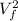`V_o^2` + 2*a*(z-
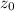`z_(0)`) for z, with
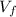`V_f`=0.