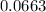Question

Suppose the time between arrivals of customers at a store closely follows an exponential distribution with a mean of 6.34 minutes.

Part A: What is the probability that the arrival of the next customer is less than 3 minutes?

Part B: What is the probability that the arrival of the next customer is more than 10 minutes?

Part C: Find the probability that the time until the arrival of the next customer is between 5 and 6 minutes.

Answer 1

Part A :
`0.3770`

Part B :
`0.2065`

Part C :
`0.0663`

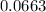
Explanation:

Let's start defining the random variable.

If X : ''Time between arrivals of customers at a store'' is the exponential random variable, its probability distribution function will be :

`f(x)=g.e^(-gx)`

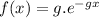
Where
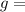`g=` λ is the parameter of the exponential distribution.

Also λ = 1 / μ where μ is the mean of the distribution.

Using the data of the exercise :

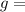`g=` λ =
`(1)/(6.34)`

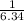
The cumulative distribution function of the exponential random variable is :

`P(X\leq x)=F(x)=1-e^(-gx)`

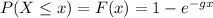
For this exercise :

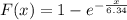`F(x)=1-e^{-(x)/(6.34)}` (I)

We are going to use the equation (I) to calculate all the probabilities.

Part A :
`P(X<3)`

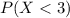
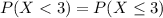`P(X<3)=P(X\leq 3)` because the exponential distribution is a continuous random variable ⇒

`P(X\leq 3)=F(3)=1-e^{-(3)/(6.34)}=1-e^{-(150)/(317)}` ≅
`0.3770`

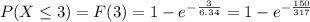Part B :
`P(X>10)` ⇒

`P(X>10)=1-P(X\leq 10)=1-F(10)` ⇒

`P(X>10)=1-(1-e^{-(10)/(6.34)})=e^{-(10)/(6.34)}` ≅
`0.2065`

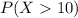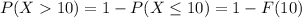Part C :
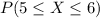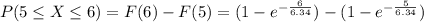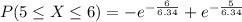`P(5\leq X\leq 6)` ⇒

`P(5\leq X\leq 6)=F(6)-F(5)=(1-e^{-(6)/(6.34)})-(1-e^{-(5)/(6.34)})` ⇒

`P(5\leq X\leq 6)=-e^{-(6)/(6.34)}+e^{-(5)/(6.34)}` ≅
`0.0663`