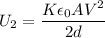Answer:
A.
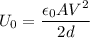
B.
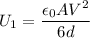
C.
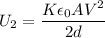
Step-by-step explanation:
The capacitance of a capacitor is its ability to store charges. For parallel-plate capacitors, this ability depends the material between the plates, the common plate area and the plate separation. The relationship is
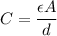
 is the capacitance,
is the capacitance,
 is the common plate area,
is the common plate area,
 is the plate separation and
is the plate separation and
 is the permittivity of the material between the plates.
is the permittivity of the material between the plates.
For air or free space,
 is
is
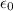 called the permittivity of free space. In general,
called the permittivity of free space. In general,
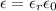 where
where
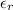 is the relative permittivity or dielectric constant of the material between the plates. It is a factor that determines the strength of the material compared to air. In fact, for air or vacuum,
is the relative permittivity or dielectric constant of the material between the plates. It is a factor that determines the strength of the material compared to air. In fact, for air or vacuum,
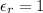 .
.
The energy stored in a capacitor is the average of the product of its charge and voltage.

Its charge,
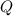 , is related to its capacitance by
, is related to its capacitance by
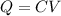 (this is the electrical definition of capacitance, a ratio of the charge to its voltage; the previous formula is the geometric definition). Substituting this in the formula for
(this is the electrical definition of capacitance, a ratio of the charge to its voltage; the previous formula is the geometric definition). Substituting this in the formula for
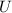 ,
,
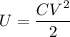
A. Substituting for
 in
in
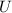 ,
,
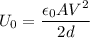
B. When the distance is
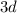 ,
,
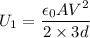
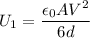
C. When the distance is restored but with a dielectric material of dielectric constant,
 , inserted, we have
, inserted, we have