Question

12) Write the equation of a rational function

Vertical asymptote at x = 0 and x = -1
Horizontal asymptote at y = -4
Hole at x = 12
X-intercepts at x = 5, x=-7 L

Answer 1

`(4(x - 5)(x + 7)(x - 12))/((x + 1)(x)(x - 12))`

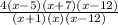
Explanation:

A rational function is

`(p(x))/(q(x))`

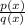
where q(x) doesn't equal zero.

If p is a asymptote, or hole at that value, then we will use

`(x - p)`

Step 1: We have asymptote as 0 and -1 so our denomiator will include

`(x - 0)(x - ( - 1)`

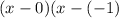
Which is

`(x)(x + 1)`

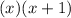
So our denomator so far is

`(p(x))/(x(x + 1))`

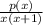
Step 2: Find Holes.

Since 12 is the value of the hole,

`(x - 12)`

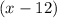
is a the binomial.

This will be both on the numerator and denomator so qe have

`((x - 12))/(x(x + 1)(x - 12))`

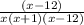
Step 3: Put the x intercepts in the numerator.

Since 5 and -7 is the intercepts,

`((x - 12)(x - 5)(x + 7))/(x(x + 1)(x - 12))`

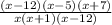
Step 4: Horinzontal Asymptotes,

Multiply the numerator and denomiator out fully,

`\frac{ {x}^(3) - 10 {x}^(2) - 59x + 420 }{ {x}^(3) - 12 {x}^(2) + x - 12}`

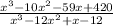
Take a L

look at the coefficients,

Notice they have the same degree,3, this means if we divide the leading coefficents, we will get our horinzonral asymptote.

Multiply the numerator by 4.

`(4(x - 12)(x - 5)(x - 7))/(x(x + 1)(x - 12))`

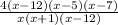
Above is the function,