Answer:
So in range "-35.6108 to 39.73"; 50% data set can be found
ux = 37.6704 unites
Explanation:
Step One: State the given parameters
From the question we are given that
mean Ц =2.06 unites
Standard deviation б is = 55.85 unites
Probability density → Normal
Let assume that it is symmetrically distributed about the mean
Step Two: Determine the range of the values
Our goal is to determine the range of values in which 50% of the data set should be found . Assuming that the range is from
 to
to
 and between these these we found 50% data set Hence from 0 up to
and between these these we found 50% data set Hence from 0 up to
 we found 25% and up to
we found 25% and up to
 we found 75% of the data set therefore z value corresponding to
we found 75% of the data set therefore z value corresponding to
 is - 0.6745 and the the z value corresponding to
is - 0.6745 and the the z value corresponding to
 is +0.6745 (Refer to the z-table for normal distribution) as shown o the diagram on the first uploaded image
is +0.6745 (Refer to the z-table for normal distribution) as shown o the diagram on the first uploaded image
The formula for z is
z =
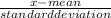
for
 ,z = - 0.6745 ,substituting into the formula
,z = - 0.6745 ,substituting into the formula
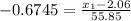
=> -37.67 =
 -2.06
-2.06
=>
 = -35.6108 unites
= -35.6108 unites
for
 , z = 0.6745 , substituting into the formula
, z = 0.6745 , substituting into the formula
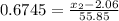
=> 37.67 =
 -2.06
-2.06
=>
 = 39.73 units
= 39.73 units
So in range "-35.6108 to 39.73"; 50% data set can be found
ux = (39.73 - (-35.73) )/2
= 37.6704 unites