Question

A jet of water squirts out horizontally from a hole on the side of the tank as shown below. 0.579 m 1.45 m h If the hole has a diameter of 3.65 mm , what is the height of the water above the hole in the tank?

Answer 1

The height of the water above the hole in the tank is 58 mm

Step-by-step explanation:

In order to solve this problem we need to draw a sketch of the dimensions that include the input variables of the problem.

Where:

x = 0.579[m]

y = 1.45 [m]

Using the following kinematic equation we can find the time that takes the water to hit the ground, and then with this time, we can find the velocity of the water in the x-component.

`y = y_(o) +v_(o) *t+(1)/(2) *g*t^(2) \\`

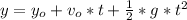
It is necessary to clarify the value of each of the respective variables below

y = - 1.45 [m] "It is negative because this point is below the water outlet"

yo = 0

vo = 0 "The velocity is zero because the component of the speed on the Y-axis does not exist"

therefore:

`-1.45=0.5*(-9.81)*t^(2) \\t = \sqrt{(1.45)/(0.5*9.81) } \\t = 0.543[s]`

The next step is to determine the velocity in component x, knowing the time.

`v=(x)/(t) \\v=(0.579)/(.543) \\v = 1.06[m/s]`

Now using torricelli's law we can find the elevation.

`v=√(2*g*h) \\h=(v^(2) )/(2*g) \\h=(1.06^(2) )/(2*9.81) \\h= 0.057[m] = 57.95[mm]`