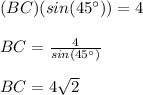Answer:
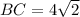
Explanation:
For this exercise you need to analize the diagram given in the exercise.
You can see that the triangle BCG is a Right triangle, because it has an angle that measures 90 degrees.
Then, you need to use the following Trigonometry Identity:
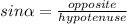
In this case you can identify that:
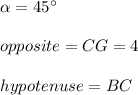
Now, you must substitute those values into
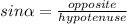 , as below:
, as below:
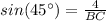
And finally, you must solve for BC in order to find its value.
Then, you get that this is: