Answer:
The magnitude of the force is 1.33 x
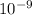 N
N
Step-by-step explanation:
In this question there are two charged body involved - the electron and the charged object. To determine the magnitude of the electrical force of the object on the electron, we use the Coulomb's law which states that:
"The force of attraction or attraction (F) between two charged bodies is the directly proportional to the product of their charges and inversely proportional to the square of the distance (r) between them."
Mathematically;
F

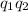 /
/

Where
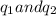 are the charges of the two bodies.
are the charges of the two bodies.
=> F = k x |
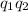 |/
|/
 -----------------(i)
-----------------(i)
Where k is a constant and has a value of k = 8.9876 ×
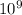 N
N
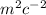
Given;
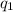 is the charge of an electron = 1.6 ×
is the charge of an electron = 1.6 ×
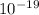 C
C
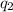 is the charge on the object = +3.0 x
is the charge on the object = +3.0 x
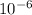 C
C
r = 0.18cm = 0.0018m
Substituting the values of k, r,
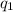 and
and
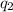 into the equation (i) above, we have;
into the equation (i) above, we have;
=> F = 8.9876 ×
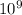 x 1.6 ×
x 1.6 ×
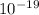 x 3.0 x
x 3.0 x
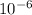 ÷
÷
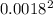
=> F = 1.33 x
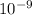 N
N