Answer:
Height = 11.975 km
Step-by-step explanation:
As we know… g = Gm/
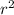 so, by substituting the values requires
so, by substituting the values requires
g = Gm/r2 = 6.673 x 10^-11 x 6.42 x 10^23 / (3397000 m)2 = 3.71 ms-1
P.E = K.E so, mgh = 1/2m
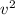
h =
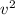 /2g = (406)2 / 2(3.71) = 11976 m or 11.975 km
/2g = (406)2 / 2(3.71) = 11976 m or 11.975 km
The bullet will travel a maximum height of 11.975 km vertically upward applying assumption of no atmosphere on the planet…