Question: Which interval contains a local minimum for the grafted function? [-4, -2.5] [-2, -1] [1, 2] [2.5, 4]
Answer:
Last option [2.5, 4]
Step-by-step explanation:
The local minima of a function are the points where the slope of the curve is zero and the function reaches a minimum value.
If, on the contrary, the function reaches a maximum value, then that point is a local maximum.
Observe, for example, the point (3, -4). Note that a line tangent to that point would be horizontal, that is, of slope m = 0. This point is a minimum of the function, because there are no values x to the right x = 3 or to the left of
x = 3 for which
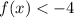
Now we must search among the options that interval contains at this point.
The intervals [-4, -2.5] [-2, -1] do not contain any local minimum
The intervalor [1, 2] contains a local maximum.
The only interval that contains a local minimum is [2.5, 4], which contains the point (3, -4)