Question

Fewer young people are driving. In year A, 61.9% of people under 20 years old who were eligible had a driver's license. Twenty years later in year B that percentage had dropped to 49.7%. Suppose these results are based on a random sample of 1,800 people under 20 years old who were eligible to have a driver's license in year A and again in year B. At 95% confidence, what is the margin of error of the number of eligible people under 20 years old who had a driver's license in year A?

Answer 1

Explanation:

Hello!

You have that the sample proportion of people under 20 years old that had a drivers licence is 0.619.

The statistic you use for a confidence interval for the population proportion is a Z and the formula for the confidence interval is

'p±
`Z_(1-\alpha /2)`*(
`\sqrt{('p(1-'p))/(n) }` )

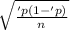The margin of error of the interval is:

d=
`Z_(1-\alpha /2)`*(
`\sqrt{('p(1-'p))/(n) }` )

d=
`Z_(0.975)`*(
`\sqrt{('p(1-'p))/(n) }` )

d=
`1.965*\sqrt{(0.619*0.381)/(1800) }`

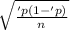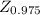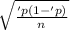d= 0.022

I hope it helps!