Question

A ball is dropped off an office building that is 790 feet tall. Apply the function h(t)=-16t^2, where h(t) is the height of the ball at the time t, and c is its initial height. Approximately how long did it take the ball to hit the ground

Answer 1

Explanation:

This models the parabolic function

`h(t)=-16t^2+v_(i)t+h_(i)`,

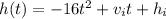where h(t) is the height after the motion occurs,
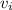`v_(i)` is the initial upwards velocity, and
`h_(i)` is the initial height from which the object was launched or dropped. Because we do not have any upwards velocity when an object is dropped straight down, it is only affected by gravity. Our function for this situation is

`h(t)=-16t^2+790`

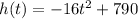
To find when the object hits the ground, replace the h(t) with a 0, since the height of something when it hits the ground has no height at all. Factor the quadratic for t, time.

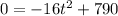`0=-16t^2+790` and

`0=-16(t^2-49.375)`

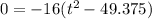
By the Zero Product Property, either

-16 = 0 or
`t^2-49.375=0`

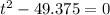
Since -16 definitely does not equal 0, then

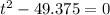`t^2-49.375=0` and

`t^2=49.375`

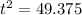
Taking the square root of both sides and only allowing for the principle (positive) root since time will never be negative, then

`t=√(49.375)` and

t = 7.03 seconds