1 Answer

Patrick White · Answer 1 · 2021-02-25T10:43:54+0000

Answer:

y(x, t) = 0.00001 [cos (
$\pi$ x - 400
$\pi$ t)]

The general equation of the displacement, y(x,t) of a wave at position x and time t and moving in the positive x-direction is given by;

y(x, t) = A cos (
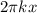$2\pi kx$ -
$2\pi ft$ )

or

y(x, t) = A cos (2
$\pi$ x/λ -
$2\pi ft$ ) -------------------(i)

Where;

k is the wave number

f is the frequency and

λ is the wavelength

A is the amplitude of the wave

=> Amplitude, A = 0.010mm

Converting this to meters, we have;

=> A = 0.00001m

=> Frequency, f = 200Hz

=> Wave speed, v = 400m/s

From the wave speed (v), we can get the wavelength (λ) of the wave as follows;

=> v = f x λ

Substitute values of f and v into the equation

=> 400 = 200 x λ

=> λ = 2m

=> Wavelength (λ) = 2m

Substituting the values of λ, A and f into equation (i) gives;

=> y(x, t) = A cos (2
$\pi$ x/2 - 2
$\pi$ (200)t)

=> y(x, t) = 0.00001 [cos (
$\pi$ x - 400
$\pi$ t)]

Therefore the y-equation for a wave travelling in the positive x-direction with frequency 200 Hz, speed 400 m/s, and amplitude 0.010 mm is given by

=> y(x, t) = 0.00001 [cos (
$\pi$ x - 400
$\pi$ t)]

where the units of x and t are respectively meters and seconds.