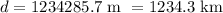Answer:
1234285.7 m or 1234.3 km
Step-by-step explanation:
Let the distance be
 , the time taken by P waves be
, the time taken by P waves be
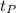 and the time taken by the S waves be
and the time taken by the S waves be
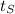 .
.
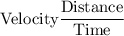
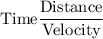
For the P waves,


For the S waves,
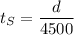
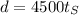
Equating the
 ,
,
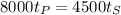
Divide both sides of the equation by 500 to reduce the terms.

Since S waves arrive 2 minutes (= 120 seconds) after P waves,
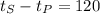
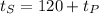
Substitute this in the equation of the distance.
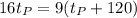
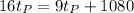

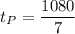
Substitute this in the equation for
 involving
involving
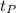 .
.