Question

Given the right triangle shown below.if Cos A =15/17 and tan A=8/15 which of the following represents the length of BC

Answer 1

The Figure for Right triangle is below,

Therefore , 15 unit length represents BC.

Explanation:

Given:

Consider a right triangle ABC, Such that

`\cos A=(15)/(17)\\\\\tan A=(8)/(15)`

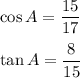
To Find:

BC = ?

Solution:

In Right Angle Triangle ABC, Cosine and Tangent identity

`\cos A = \frac{\textrm{side adjacent to angle C}}{Hypotenuse}\\`

`\tan A= \frac{\textrm{side opposite to angle A}}{\textrm{side adjacent to angle A}}`

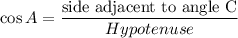
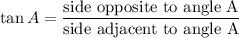
BUT,

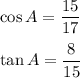`\cos A=(15)/(17)\\\\\tan A=(8)/(15)` ....Given

On Comparing,

Adjacent side to angle A = AB = 15

Opposite side to angle A = BC = 8

Hypotenuse = AC =17

Also Pythagoras theorem is Satisfies,

`(\textrm{Hypotenuse})^(2) = (\textrm{Shorter leg})^(2)+(\textrm{Longer leg})^(2)`

`(\textrm{Hypotenuse})^(2) = 17^(2)=289`

`(\textrm{Shorter leg})^(2)+(\textrm{Longer leg})^(2)=15^(2)+8^(2)=289`

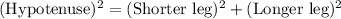
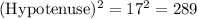
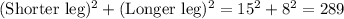
The Figure for Right triangle is below,

Therefore , 15 unit length represents BC.