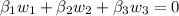Since
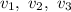 are linearly dependent, there exist coefficients
are linearly dependent, there exist coefficients
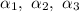 such that
such that
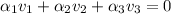
Now, a linear combination of the new vectors would look like this:
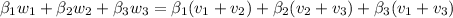
Which simplifies to
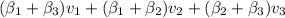
So, any linear combination of
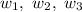 is also a linear combination of
is also a linear combination of
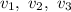 . This implies that we can choose the coefficients for a linear combination that will give the zero vector.
. This implies that we can choose the coefficients for a linear combination that will give the zero vector.
In particular, if
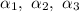 are the coefficients such that
are the coefficients such that
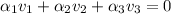
we can choose
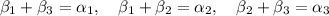
And we have