Step-by-step explanation:
The given data is as follows.
Pulling force on the reel is F = T = 2.3 N
Mass of cylinder (m) = 0.82 kg
Radius of cylinder (r) = 0.045 m
Formula for torque pulling force on the cylinder is as follows.
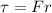
=

Moment of inertia of the cylinder (I) is as follows.
I =
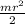
 = angular acceleration of the cylinder
= angular acceleration of the cylinder
Hence,
Fr =
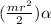
or,
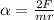
=
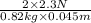
= 124.66
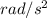
Amount of line pulled is h and it is in a times of 0.2 sec.
Now, linear acceleration is calculated as follows.
a =
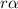
=
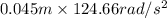
= 5.61
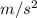
Now, relation between h and acceleration as follows.
h =
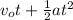
here,
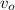 = 0
= 0
Hence, calculate the value of h as follows.
h =
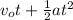
=
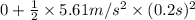
= 0.1121 m
Thus, we can conclude that acceleration of the fishing reel is 5.61
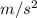 and it will pull 5.61
and it will pull 5.61
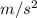 line from the reel in 0.20 s.
line from the reel in 0.20 s.