Question

A committee of 6 people is to be chosen from a group consisting of 7 men and 8 women. If the committee must consist of at least 3 women and at least 2 men, how many different committees are possible?

Answer 1

The total number of possible committees are 3430.

Explanation:

In this Question we have a committee of 6 from 7 men and 8 women.

but already have fixed number of men and women in the committees so.

we will use combinations with each men and women to fill the criteria of the committee. we have two cases as the number of men and women in the committee is fixed.

1) the remaining person is a man.

2)the remaining person is a women.

Now taking the women candidates as fixed such that the remaining 6th person is a man As for 3 women that can be chosen from 8 women candidates are
`\left \{ {{8} \atop {3}} \}\right` and also for 3 men in 7 men candidates will be
`\left \{ {{7} \atop {3}} \}\right.`

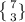
now, by multiplying both terms we get value of 1960 combinations.

In second case we need to make combinations for 4 women candidates with fixed value of man of 2 candidates such that the remaining 6th person is a women.

So for 3 man (fixed ) the combination will be
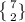`\left \{ {{7} \atop {2}} \}\right.` and for 4 women candidates it is
`\left \{ {{8} \atop {4}} \}\right.` which by multiplying gives us the answer as 1470.

Now adding the possible combinations we get 3430 combinations

i.e.

`\left \{ {{8} \atop {3}} \}\right. \left \{ {{7} \atop {3}}\} \right. + \left \{ {{8} \atop {4}} \}\right. \left \{ {{7} \atop {2}}\} \right. =3430`

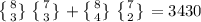
thank you.