Question

Quartiles divide a sample into four nearly equal pieces. In general. a sample of size n can be broken into k nearly equal pieces by using the cut points (1 / k) (n + 1) for ? = 1, . . . . k ? 1. Consider the following ordered sample: 2 182341 44 464961 62 74 76 79 82 89 92 95 a. Tertiles divide a sample into thirds. Find the tenues of this sample. b. Quintiles divide a sample into fifths. Find the quintiles of this sample.

Answer 1

For this answer, the cut points will be expressed as:

`\\ (j*(n+1))/(k)`

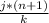
And the values are as follows:

`\\ L = {2, 18, 23, 41, 44, 46, 49, 61, 62, 74, 76, 79, 82, 89, 92, 95}`

Answer:

a. Tertiles are 45.334 and 76.999; b. Quintiles are 30.20, 48.40, 74.40, 86.20.

Explanation:

To find the tertiles (or terciles), quintiles, percentiles, and so on, that is, for tertiles are two values that divide the sample into three equal parts (or each containing a third part of the population of values); for quintiles are four values that divide the sample into five equal parts, we can use the general formula proposed for some authors (Dodge, Y., (2008). The Concise Encyclopedia of Statistics):

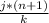`\\ (j*(n+1))/(k)` (1)

Where j is the jth-element of a quantile, n is the number of the elements in the list and k is the number of parts in which we can divide the values of the ordered list of elements of the population (2-quantile=median, 3-quantile=tertile, 5-quantile=quintiles, 100-quantile=percentiles). In this case, k = 3 (tertiles) and k = 5(quintiles).

Well, for calculating the tertiles or quintiles, the only difference will be the value k in the equation (1). The general procedure for finding the tertiles and quintiles is as follows:

Order the values in increasing order.

l will be the integer part of
`\\ (j*(n+1))/(k)`.

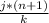m will be the fraction part of
`\\ (j*(n+1))/(k)`.

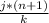Then, considering the next expression:

`\\ Q_(j)= x_(l) + m*(x_(l+1)-x_(l))`

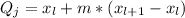
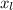`\\ x_(l)` is the observation or value corresponding to the lth position.

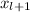`\\ x_(l+1)` is the observation or value corresponding to the (l+1)th position.

Then, the jth tertiale is:

`\\ T_(j)= x_(l) + m*(x_(l+1)-x_(l))`

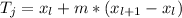
And the jth quintile is:

`\\ q_(j)= x_(l) + m*(x_(l+1)-x_(l))`

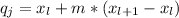
Calculating the tertiles

The first tertile, using the equation (1) is:

n=16 (elements of the list), k=3 (tertiles), j=1 (first tertile).

`\\ (j*(n+1))/(k)`

`\\ (1*(16+1))/(3)`

`\\ (17)/(3)=5.667`

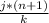
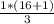
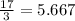
Then, l (integer part) = 5; m(fraction part) =0.667.

As a result, the first tertile is:

`\\ T_(j)= x_(l) + m*(x_(l+1)-x_(l))`

`\\ T_(1)= x_(5) + 0.667*(x_(5+1)-x_(5))`

`\\ T_(1)= x_(5) + 0.667*(x_(6)-x_(5))`

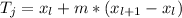
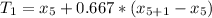
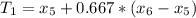
Looking at the list in increasing order:

`\\ L = {2, 18, 23, 41, 44, 46, 49, 61, 62, 74, 76, 79, 82, 89, 92, 95}`

The 5th element = 44; the 6th element = 46.

`\\ T_(1)= 44 + 0.667*(46-44)`

`\\ T_(1)= 45.334`

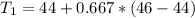
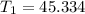
Following the same procedure, the second tertile is:

`\\ (2*(16+1))/(3)=(2*17)/(3)=11.333`

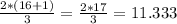
Then, l (integer part) = 11; m(fraction part) =0.333.

`\\ T_(2)= x_(11) + 0.333*(x_(11+1)-x_(11))`

`\\ T_(2)= x_(11) + 0.333*(x_(12)-x_(11))`

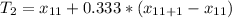
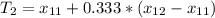
The 11th element is 76; the 12th element = 79.

`\\ T_(2)= 76 + 0.333*(79-76)`

`\\ T_(2)= 76 + 0.333*(79-76)`

`\\ T_(2)= 76.999`

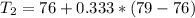
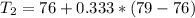
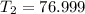
Thus, the tertiles are 45.334 and 76.999.

Calculating the quintiles

The same procedure as previously explained.

The first quintile:

`\\ (j*(n+1))/(k)`

`\\ (1*(16+1))/(5)=(17)/(5)=3.4`

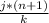
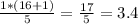
Thus, l (integer part) = 3; m(fraction part) = 0.4.

`\\ q_(1)= x_(3) + 0.4*(x_(3+1)-x_(3))`

`\\ q_(1)= x_(3) + 0.4*(x_(4)-x_(3))`

`\\ q_(1)= 23 + 0.4*(41-23)`

`\\ q_(1)= 30.2`

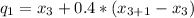
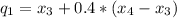
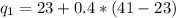
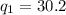
The second quintile:

`\\ (j*(n+1))/(k)`

`\\ (2*(17))/(5)=6.80`

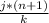
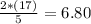
Thus, l (integer part) = 6; m(fraction part) = 0.8.

`\\ q_(2)= x_(6) + 0.8*(x_(6+1)-x_(6))`

`\\ q_(2)= x_(6) + 0.8*(x_(7)-x_(6))`

`\\ q_(2)= 46 + 0.8*(49-46)`

`\\ q_(2)= 48.40`

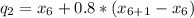
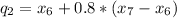
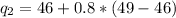
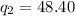
The third quintile:

`\\ (j*(n+1))/(k)`

`\\ (3*(17))/(5)=10.20`

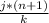
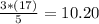
Thus, l (integer part) = 10; m(fraction part) = 0.20.

`\\ q_(3)= x_(10) + 0.2*(x_(11)-x_(10))`

`\\ q_(3)= 74 + 0.2*(76-74)`

`\\ q_(3)= 74.40`

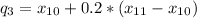
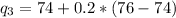
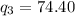
And finally, the fourth quintile:

`\\ (j*(n+1))/(k)`

`\\ (4*(17))/(5)=13.60`

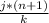
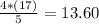
Thus, l (integer part) = 13; m(fraction part) = 0.60.

`\\ q_(4)= x_(13) + 0.6*(x_(14)-x_(13))`

`\\ q_(4)= 82 + 0.6*(89-82)`

`\\ q_(4)= 86.20`

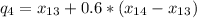
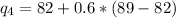
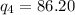
Thus, the quintiles are 30.20, 48.40, 74.40 and 86.20.