Question

Two computers are connected to a password-protected wireless network. When the password is temporarily removed, a virus can attack the first computer with probability 0.5, the second computer with probability 0.7, and it can attack both computers with probability 0.4.

a.The first computer appears infected with a virus. What is the probability that the second computer was also attacked?
b.The first computer was not attacked at all. What is the probability that the second computer was attacked?

Part a is .8.
I need part b. Please thouroughly explain. I keep getting 0.6, which is marked wrong. IF YOU GET .6, thoroughly explain.

Answer 1

Explanation:

Hello!

You have two computers connected to a password-protected wireless network.

Let's call the first computer "A" and the second computer "B", if you take the password, the computers can be affected by a virus following the probabilities:

P(A)= 0.5

P(B)= 0.7

P(A∩B)= 0.4

a. This is a conditional probability, the first computer is already infected, what is the probability of the second being affected, symbolically:

P(B/A)

Applying the definition of conditional probability you know that:

`P(B/A)= (P(BnA))/(P(A))`

`P(B/A)= (0.4)/(0.5) = 0.8`

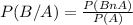
b. Since the first item asks for a conditional probability it seems logical to think that you need to use the same procedure for this one. Truth is that you already know what is the probability of the second computer being infected, there is no need to do any calculation. P(B)= 0.7

I hope you have a SUPER day!